Dùng VBA trong EXCELL tìm điểm A trong Autocad (6 người xem)

tranvanhung2009 · 13/12/19

Xin chào cả nhà.
Mình có 1 file cad chứa 1 đường tròn O bán kính OF. Đã biết chiều dài cung IA = c xuất phát từ điểm I(a,b). Đường thẳng l đi qua I vuông góc với trục Ox.
Mình cần dùng VBA trong Excell dùng vòng lặp để xác định điểm A với điều kiện: Điểm A thuộc đường tròn tâm O bán kính F và đường thẳng l tiếp tuyến với cung IA tại I.
Rất mong mọi người giúp đỡ.

VetMini · 13/12/19

tranvanhung2009 đã viết:
...
Mình cần dùng VBA trong Excell dùng vòng lặp để xác định điểm A với điều kiện: Điểm A thuộc đường tròn tâm O bán kính F và đường thẳng l tiếp tuyến với cung IA tại I.
Rất mong mọi người giúp đỡ.

VBA là bản quyền của Microsoft. Tôi không chắc cái phần mềm Excell gì đó chạy được đâu.

ppc0312 · 13/12/19

tranvanhung2009 đã viết:
Xin chào cả nhà.
Mình có 1 file cad chứa 1 đường tròn O bán kính OF. Đã biết chiều dài cung IA = c xuất phát từ điểm I(a,b). Đường thẳng l đi qua I vuông góc với trục Ox.
Mình cần dùng VBA trong Excell dùng vòng lặp để xác định điểm A với điều kiện: Điểm A thuộc đường tròn tâm O bán kính F và đường thẳng l tiếp tuyến với cung IA tại I.
Rất mong mọi người giúp đỡ.

Nếu là CAD, tốt nhất dùng VBA trong CAD, hoặc dùng ngôn ngữ LISP để làm
Và trên hết nên sang diễn đàn CAD sẽ nhanh và chuyên hơn

befaint · 13/12/19

Excel và AutoCAD có mối quan hệ khá thân thiết.

Có khá nhiều addins làm việc qua lại giữa hai phần mềm này.

VetMini · 13/12/19

befaint đã viết:
Excel và AutoCAD có mối quan hệ khá thân thiết.
Có khá nhiều addins làm việc qua lại giữa hai phần mềm này.

Thớt hỏi VBA cho Excell mà.
Tên phần mềm còn không rõ nữa thì cốt kiếc chi cho mệt.

batman1 · 13/12/19

Thực ra bài toán là xác định tọa độ của A, tức đơn thuần là tính toán. Tính toán thì tính ở đâu cũng được, và thực ra chẳng cần vòng lặp gì cả.

Bài toán với phát biểu hiện tại thì không xác định. Có 2 đường tròn cùng tiếp xúc với l tại điểm I. Chúng nằm ở 2 phía của đường thẳng l, đối xứng với nhau qua trục l.

Cũng nên cho biết a và b âm hay dương. Tức điểm I nằm ở phần tư thứ I, II, III hay IV của mặt phẳng toạ độ (mặt phẳng tọa độ được chia làm 4 phần tư bởi 2 trục x và y).

Tôi viết những điều trên (2 đường tròn, a và b âm dương) khi chưa tải tập tin. Vì hiện tại tôi chưa tải được tập tin do máy có trục trặc.
--------------------------------
Tôi đã tải được tập tin nhưng đó là tập tin của AutoCAD mà tôi lại không có để mở. Nếu muốn tính toán tọa độ của A dùng Excel thì phải có: bán kính đường tròn r (đã cho), độ dài cung IA = c (đã cho), đường tròn và gốc toạ độ nằm cùng phía hay khác phía so với đường thẳng l (chưa cho).

Còn một điều tôi quên là thậm chí xác định được đường tròn và gốc tọa độ nằm cùng phía hay khác phía so với đường thẳng l thì luôn có 2 điểm A thỏa điều kiện. Chúng nẳm đối xứng với nhau qua trục k, với k là đường thẳng vuông góc với l và đi qua điểm I. Bạn định tính tọa độ cho điểm A nào (chưa cho)?

tranvanhung2009 · 14/12/19

ppc0312 đã viết:
Nếu là CAD, tốt nhất dùng VBA trong CAD, hoặc dùng ngôn ngữ LISP để làm
Và trên hết nên sang diễn đàn CAD sẽ nhanh và chuyên hơn

Vì

batman1 đã viết:
Thực ra bài toán là xác định tọa độ của A, tức đơn thuần là tính toán. Tính toán thì tính ở đâu cũng được, và thực ra chẳng cần vòng lặp gì cả.

Bài toán với phát biểu hiện tại thì không xác định. Có 2 đường tròn cùng tiếp xúc với l tại điểm I. Chúng nằm ở 2 phía của đường thẳng l, đối xứng với nhau qua trục l.

Cũng nên cho biết a và b âm hay dương. Tức điểm I nằm ở phần tư thứ I, II, III hay IV của mặt phẳng toạ độ (mặt phẳng tọa độ được chia làm 4 phần tư bởi 2 trục x và y).

Tôi viết những điều trên (2 đường tròn, a và b âm dương) khi chưa tải tập tin. Vì hiện tại tôi chưa tải được tập tin do máy có trục trặc.
--------------------------------
Tôi đã tải được tập tin nhưng đó là tập tin của AutoCAD mà tôi lại không có để mở. Nếu muốn tính toán tọa độ của A dùng Excel thì phải có: bán kính đường tròn r (đã cho), độ dài cung IA = c (đã cho), đường tròn và gốc toạ độ nằm cùng phía hay khác phía so với đường thẳng l (chưa cho).

Còn một điều tôi quên là thậm chí xác định được đường tròn và gốc tọa độ nằm cùng phía hay khác phía so với đường thẳng l thì luôn có 2 điểm A thỏa điều kiện. Chúng nẳm đối xứng với nhau qua trục k, với k là đường thẳng vuông góc với l và đi qua điểm I. Bạn định tính tọa độ cho điểm A nào (chưa cho)?

Cám ơn bác đã đọc bài.
Vì cần dùng VBA để mình tính ra được nhiều điểm A trên excell
Em dự kiến sẽ xuất các tâm và bán kính ra exell. Sau đó sẽ dùng vòng lặp trong VBA để tính toàn bộ điểm A.
Em đã đưa về dạng file cell để mọi người có thể tiện xem ạ

batman1 · 14/12/19

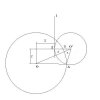
Bây giờ có hình thì mới thấy hơi khác với cái mà tôi tưởng tượng trước khi có hình. Nhưng ta đã biết:
- tọa độ của tâm O là (0; 0), tức tâm O nằm ở gốc tọa độ.
- điểm I nằm ở phần tư I của mặt phẳng tọa độ.
- tâm O và O' nằm ở 2 phía khác nhau của đường thẳng l.
- đường tròn O' tiếp xúc với l tại điểm I, tâm O' nằm trên đường thẳng song song với trục Ox và đi qua điểm I.

Theo tôi thì làm như sau ...

Gọi góc OO'A là α, góc IO'O là α'. α và α' đều tính bằng radian. Gọi bán kính đường tròn O' là R, bán kính đường tròn O là r.

TAN(α') = y/(x + R)
=> α' = ATAN(y/(x + R))

Theo định lý cos trong tam giác OO'A có: r² = R² + OO'² - 2*R*OO'*cos(α)
=> cos(α) = (R² + OO'² - r²) / (2*R*OO')
=> α = ACOS((R² + OO'² - r²) / (2*R*OO'))

Góc IO'A = α' + α = ATAN(y/(x + R)) + ACOS((R² + OO'² - r²) / (2*R*OO')) *

Ta biết rằng góc ở tâm O' có độ lớn 1 radian thì chắn cung có chiều dài bằng bán kính đường tròn, vậy góc IO'A = α' + α chắn cung IA có độ lớn bằng R*(α' + α)

=> cung_IA = R*(α' + α) = R*ATAN(y/(x + R)) + ACOS((R² + OO'² - r²) / (2*R*OO')) **

Theo Pitago thì OO'² = y² + ̣(x + R)² => OO' = √(y² + ̣(x + R)²)

Thay các giá trị OO'² và OO' vào ** ta có:

cung_IA = R*ATAN(y/(x + R)) + ACOS((R² + y² + ̣(x + R)² - r²) / (2*R*√(y² + ̣(x + R)²))) ***

Như vậy cung_IA là hàm một biến R (x, y, r cho trước).

Công việc:
- Ta chọn giá trị R đủ lớn (hoặc R = r - x)
- Trong vòng lặp FOR giảm dần giá trị R (hoặc tăng dần giá trị R)
- Với mỗi vòng FOR tính giá trị cung_IA theo công thức ***. Nếu giá trị cung_IA khác giá trị cung IA cho trước không quá một sai số cho trước (đủ nhỏ) thì kết thức vòng lặp.

Gọi H là chân đường vuông góc hạ từ A xuống IO' ta có:
- HO' = R*cos(α' + α) ****
- AH = R*sin(α' + α) *****

Tính được R rồi thì tính được α' + α theo *, và theo **** tính được HO', theo ***** tính được AH

Tọa độ x của A = x + R - HO'
Tọa độ y của A = -(AH - y)

Hi vọng không nhầm lẫn.

tranvanhung2009 · 14/12/19

Em thấy hướng đi của bác rất ổn.
Đây là file Excel của em cần viết vòng lặp để tính điểm A.
Bác batman1 xem và giúp đỡ ạ

ppc0312 · 15/12/19

tranvanhung2009 đã viết:
Vì

Vì ... cái đó của người khác đâu phải của bạn
Trong CAD có hàm và nhiều lệnh hỗ trợ tiếp tuyến luôn, thay vì phải giải dạng giải tích như trong Excel

batman1 · 15/12/19

tranvanhung2009 đã viết:
Em thấy hướng đi của bác rất ổn.
Đây là file Excel của em cần viết vòng lặp để tính điểm A.
Bác batman1 xem và giúp đỡ ạ

Trước hết về sơ suất. Trong bài #8 do sơ suất mà tôi dùng thiếu cặp dấu ().
1. Không phải
cung_IA = R*(α' + α) = R*ATAN(y/(x + R)) + ACOS((R² + OO'² - r²) / (2*R*OO')) **

mà phải là

cung_IA = R*(α' + α) = R*(ATAN(y/(x + R)) + ACOS((R² + OO'² - r²) / (2*R*OO'))) **

2. Không phải
cung_IA = R*ATAN(y/(x + R)) + ACOS((R² + y² + ̣(x + R)² - r²) / (2*R*√(y² + ̣(x + R)²))) ***

mà phải là

cung_IA = R*(ATAN(y/(x + R)) + ACOS((R² + y² + ̣(x + R)² - r²) / (2*R*√(y² + ̣(x + R)²))))***
---------------
Tôi không biết dữ liệu của bạn có cùng đơn vị không. Giả sử đơn vị trục là một đoạn nào đó (1 mm, 2 cm, 5 m - tùy ý - được lấy làm đơn vị trên trục Ox và Oy). Lúc đó dữ liệu đầu vào phải cho với cùng 1 đơn vị trục. Vd. r = 50, Ix = 23, Iy = 10, cungIA = 123 thì có nghĩa: bán kính = 50 đơn vị, Ix = 23 đơn vị, Iy = 10 đơn vị, và cungIA = 123 đơn vị.

Nếu các con số trong dữ liệu được cho với cùng 1 đơn vị đo lường thì tôi thấy có dữ liệu có vẻ vô lý. Theo đánh giá sơ bộ của tôi thì cung IA của đường tròn O' không thể lớn hơn đường kính của đường tròn O. Trong khi đó thì dữ liệu tôi nêu trên cho thấy cung IA = 123 > 100 = đường kính của đường tròn O.

Tôi không biết bạn lấy dữ liệu từ đâu, và chúng có tồn tại không. Bạn có chắc là có dữ liệu thực như dòng 6 trong tập tin, và bạn cần tính tọa độ của điểm A? Hay bạn muốn thử tìm xem liệu có vòng tròn O' thỏa điều kiện là cho cung IA = 123, và nếu thỏa thì tính tọa độ điểm A?

Bạn xem tập tin tôi đính kèm. Tôi dùng sai số là sai_so = 0.1. Trước khi vào vòng lặp thì bán kính vòng tròn O' được đặt R1 = r - Ix . Trong mỗi vòng lặp nếu so sánh không thỏa thì R1 được tăng thêm một lượng bằng buoc_nhay = 1. Cả sai_so va buoc_nhay đều có thể thay đổi khi gọi hàm tinh_cung. Để có thể ra khỏi vòng lặp khi không tìm thấy thì code chỉ xét bán kính đường tròn O' không lớn hơn 500 lần bán kính đường tròn O. Khi tăng dần bán kính đường tròn O' mà vượt 500 lần bán kính đường tròn O thì ra khỏi vòng lặp. Nếu tìm thấy thì ra khỏi vòng lặp.

Để test thì chạy sub toadoA.

Tôi không còn gì để nói thêm nữa. Nếu cần thì bạn hãy tự tìm nhé.

tranvanhung2009 · 15/12/19

batman1 đã viết:
Trước hết về sơ suất. Trong bài #8 do sơ suất mà tôi dùng thiếu cặp dấu ().
1. Không phải
cung_IA = R*(α' + α) = R*ATAN(y/(x + R)) + ACOS((R² + OO'² - r²) / (2*R*OO')) **

mà phải là

cung_IA = R*(α' + α) = R*(ATAN(y/(x + R)) + ACOS((R² + OO'² - r²) / (2*R*OO'))) **

2. Không phải
cung_IA = R*ATAN(y/(x + R)) + ACOS((R² + y² + ̣(x + R)² - r²) / (2*R*√(y² + ̣(x + R)²))) ***

mà phải là

cung_IA = R*(ATAN(y/(x + R)) + ACOS((R² + y² + ̣(x + R)² - r²) / (2*R*√(y² + ̣(x + R)²))))***
---------------
Tôi không biết dữ liệu của bạn có cùng đơn vị không. Giả sử đơn vị trục là một đoạn nào đó (1 mm, 2 cm, 5 m - tùy ý - được lấy làm đơn vị trên trục Ox và Oy). Lúc đó dữ liệu đầu vào phải cho với cùng 1 đơn vị trục. Vd. r = 50, Ix = 23, Iy = 10, cungIA = 123 thì có nghĩa: bán kính = 50 đơn vị, Ix = 23 đơn vị, Iy = 10 đơn vị, và cungIA = 123 đơn vị.

Nếu các con số trong dữ liệu được cho với cùng 1 đơn vị đo lường thì tôi thấy có dữ liệu có vẻ vô lý. Theo đánh giá sơ bộ của tôi thì cung IA của đường tròn O' không thể lớn hơn đường kính của đường tròn O. Trong khi đó thì dữ liệu tôi nêu trên cho thấy cung IA = 123 > 100 = đường kính của đường tròn O.

Tôi không biết bạn lấy dữ liệu từ đâu, và chúng có tồn tại không. Bạn có chắc là có dữ liệu thực như dòng 6 trong tập tin, và bạn cần tính tọa độ của điểm A? Hay bạn muốn thử tìm xem liệu có vòng tròn O' thỏa điều kiện là cho cung IA = 123, và nếu thỏa thì tính tọa độ điểm A?

Bạn xem tập tin tôi đính kèm. Tôi dùng sai số là sai_so = 0.1. Trước khi vào vòng lặp thì bán kính vòng tròn O' được đặt R1 = r - Ix . Trong mỗi vòng lặp nếu so sánh không thỏa thì R1 được tăng thêm một lượng bằng buoc_nhay = 1. Cả sai_so va buoc_nhay đều có thể thay đổi khi gọi hàm tinh_cung. Để có thể ra khỏi vòng lặp khi không tìm thấy thì code chỉ xét bán kính đường tròn O' không lớn hơn 500 lần bán kính đường tròn O. Khi tăng dần bán kính đường tròn O' mà vượt 500 lần bán kính đường tròn O thì ra khỏi vòng lặp. Nếu tìm thấy thì ra khỏi vòng lặp.

Để test thì chạy sub toadoA.

Tôi không còn gì để nói thêm nữa. Nếu cần thì bạn hãy tự tìm nhé.

Chân thành cám ơn bác.
Chúc bác sức khỏe và có nhiều đóng góp cho diễn đàn
Một lần nữa rất cám ơn bác!

Dùng VBA trong EXCELL tìm điểm A trong Autocad (6 người xem)

Người dùng đang xem chủ đề này

tranvanhung2009

Thành viên hoạt động

File đính kèm

VetMini

Ăn cùng góc phố

ppc0312

whom?

befaint

|||||||||||||

VetMini

Ăn cùng góc phố

batman1

Thành viên gạo cội

tranvanhung2009

Thành viên hoạt động

File đính kèm

batman1

Thành viên gạo cội

tranvanhung2009

Thành viên hoạt động

File đính kèm

ppc0312

whom?

batman1

Thành viên gạo cội

File đính kèm

tranvanhung2009

Thành viên hoạt động

Bài viết mới nhất

Thành viên có số lượng bài viết cao nhất tháng

Thành viên có điểm tương tác cao nhất tháng

Đếm ngược thời gian