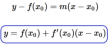Biểu diễn Tiếp Tuyến Của Đường Cong Trong Đồ Thị Của Excel (3 người xem)

[Ly-Hansen]

Chào các anh chị và các bạn!
Xin nhờ các anh chị và các bạn chỉ giùm làm sao để biểu hiện tiếp tuyến của Đường Cong như hình dưới đây voi nhé. Mình xin chân thành cảm ơn!!

 

[ptm0412]

Làm từng bước:
- Viết hàm Linest (hồi quy) để có các hệ số a, b, c của đường cong biểu diễn hàm số. Hoặc vẽ đường trend line để lấy biểu thức hàm số
- Viết đạo hàm bậc nhất của hàm số đó, lấy hệ số a và b
- Thế 1 giá trị b1 vào hàm của đạo hàm, tính ra a và b của đường tiếp tuyến tại điểm b1.
- Tạo dữ liệu 3 điểm cho đường tiếp tuyến tại x = b1, x = b1 -1, x = b1 +1
- Vẽ đồ thị 3 điểm này (serie mới)
- Thực hiện cho các giá trị b tiếp theo.

 

[Ly-Hansen]

Cảm ơn bạn Cheettit! Vấn đề là, vẽ đồ thị từ bảng giá trị cho trước như dưới đây ah. Thanks!

 

[ptm0412]

Vấn đề là, vẽ đồ thị từ bảng giá trị cho trước như dưới đây ah. Thanks!

Đừng có ah với thanks với tôi, tôi không hiểu. Thì cứ vẽ đồ thị trước đi, sau đó làm các bước như bài 2.

 

[PhanTuHuong]

Vấn đề này không phải của Excel mà là kiến thức của lượng giác

 

[ptm0412]

Vấn đề này không phải của Excel mà là kiến thức của lượng giác

Là đạo hàm và vi phân (giải tích).
Đạo hàm bậc nhất là hệ số góc (a) của đường tiếp tuyến y = ax + b

 

[huhumalu]

Là đạo hàm và vi phân.
Đạo hàm bậc nhất là hệ số góc (a) của đường tiếp tuyến y = ax + b

Xin phép anh để diễn giải thêm
1. Lý thuyết
Hệ số góc của tiếp tuyến tại vị trí A(x0, f(x0)), là giá trị cho bởi đạo hàm bậc 1 của hàm fx tại vị trí x0.

​

điểm đang xét là tiếp điểm do vậy vừa thuộc đường tiếp tuyến vừa thuộc hàm số. Đường thẳng như đã nói ở trên có hệ số góc là m.
Ta được phương trình đường thẳng tiếp tuyến tại x0

​

2. Áp dụng vào số liệu tại #3
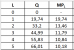
Từ bảng số liệu trên ta dùng các hàm hồi quy (TREND, FORECAST, LINEST, SLOPE và INTERCEPT) để tìm ra phương trình đường cong gần đúng thể hiện lại các số liệu trên.
--> Tìm ra fx (bậc n, hoặc Logarit, tùy thuộc vào số liệu ...)
Rồi làm các bước như bài #2
+ Ta có phương trình đường thẳng f(x), ta đạo hàm bậc 1, được f'(x)
+ Gọi các tiếp điểm là (0), (1), (2), ... hoành độ các tiếp điểm ta sẽ vẽ tiếp tuyến là x0, x1, x2, ... ta chọn luôn là các giá trị cột MPL
+ Có x0, x1, x2, ... thay vào phương trình khoanh màu xanh bên trên --> Ta được phương trình đường thẳng [PT] y0, y1, y2, ... Hay là phương trình tiếp tuyến tại điểm (0), (1), (2), ...
+ Vì trong đồ thị của excel không vẽ được đường thẳng dựa vào phương trình [PT], mà vẽ đoạn thẳng đi qua các điểm. Mà vẽ cả phương trình đường thẳng vào thì rối, do vậy ta chỉ vẽ các đoạn. Vậy ta đi tìm đầu mút các đoạn tiếp tuyến, có phương trình rồi, thì từ x0 ta lấy sang bên trái và bên phải x0, một đoạn có giá trị bằng 1 (hoặc to hơn thì tùy vào số liệu) --> nghĩa là x0 - 1 ; và x0 +1 ; có 2 tung độ này, thay vào đường thẳng [PT], là ta đủ 3 điểm của đoạn thẳng tiếp tuyến, ta đưa vào biểu đồ thôi.
+ Lặp lại cho x1, x2, ....

 

[VetMini]

Vấn đề là tại điểm chỉ cần cho biết tan của góc (đạo hàm) thôi là đủ rồi. Vẽ ba cái tiếp tuyến chi vậy?
Như hình tring bài #1 chỉ thấy một cục rồi nùi chứ có làm đẹp đẽ, rõ rệt gì thêm đâu.

 

[ptm0412]

Vấn đề là tại điểm chỉ cần cho biết tan của góc (đạo hàm) thôi là đủ rồi. Vẽ ba cái tiếp tuyến chi vậy?
Như hình trong bài #1 chỉ thấy một cục rối nùi chứ có làm đẹp đẽ, rõ rệt gì thêm đâu.

Lại còn 1 việc nữa: Khi hồi quy bằng excel, sẽ có việc phương trình hồi quy không chính xác như biểu đồ số liệu thực, khiến cho đường trend của biểu đồ không trùng khớp với đường biểu diễn số liệu thực. Dùng hàm hồi quy xong vẽ lên nó lệch ra khỏi biểu đồ, không đúng như mong muốn.
--------
Vẽ trend line phải làm đúng:
- Chọn dạng hàm số đúng
- Kiểm tra "độ chặt" R, càng gần 1 càng tốt
Dữ liệu cần càng nhiều điểm càng tốt. Dữ liệu 5 con số, biểu đồ 5 points thì hồi quy không thể chính xác.