Thư Sinh Áo Trắng
Thành viên hoạt động



- Tham gia
- 26/3/21
- Bài viết
- 160
- Được thích
- 31






Vâng bác! Vậy Log trong VBA là Logarit cơ số e luôn.Hàm Log tự nhiên trong VBA là Log(số)
Trừ phi bạn muốn làm con tính theo chuỗi khai triển Taylor. (Tính theo chuỗi Taylor cũng xứng đáng làm một bài tập viết code)Vâng bác! Vậy Log trong VBA là Logarit cơ số e luôn.




Bài 1 minh họa cho câu hỏi để các bác có để ý đến thì dễ hiểu bác ạ!Bảng tính mà còn bày đặt merge cells chỉ tổ gặp rắc rối sau này.
Bỏ merge cells đi thì mới có hứng code.
Bảng tạo Đích tạo ra là bảng có giá trị sau khi Log(x) là được ạ, không phải là tham chiếu Formula1. dùng Record Macro để chọn nguyên vùng nguồn
2. dùng Record Macro để chọn nguyên vùng đích, gõ công thức vào ô đầu và Ctrl+Enter để nó cóp công thức sang các ô còn lại.
3. chỉnh macro. Hàm Log tự nhiên trong VBA là Log(số). Hàm log theo hệ là Log(số)/Log(hệ)
Do dính dáng đến hồi quy phi tuyến nên Loga nê pe 2 vế đưa về tuyến tính.Nên Loga nê pê bảng dữ liệu đầu vào để hồi quy phi tuyến theo tuyến tính.Trừ phi bạn muốn làm con tính theo chuỗi khai triển Taylor. (Tính theo chuỗi Taylor cũng xứng đáng làm một bài tập viết code)
Cóp từ quép sai chỉ dẫn của Microsoft:
View attachment 259856
Dịch:
Hàm trả về một trị Double là Log tự nhiên của một số.
Ngữ pháp:
Log(số)
Số là tham bắt buộc, kiểu biến Double hoặc bất kỳ biểu thức số lớn hơn 0.
Chú của riêng tôi: VBA có tậ ép kiểu, chỉ cần cho nó tham là số thì nó tự đọng ép ra Double. Vả lại, Double là kiểu cao nhất của số cho nên hầu như bất cứ số nào cũng có thể ép thành Double tư. Tuy nhiên, nếu gọi hàm này với hằng thì nên thêm # sau hằng để trình dịch khỏi phải ép kiểu
Log(15#)
Chú thích:
Log tự nhiên là log với hệ e. Hằng số e có giá trị khoảng 2,718282.



Có cái nội suy đa thức sự phiền các bác không dám đưa lên.Sub t()
Const RGNGU = "c3" ' từ đây xác định vùng sử dụng của đầu vào
Const RGNGUOFFSET = 2 ' vùng sử dụng sẽ chứa 2 dòng title, dữ liệu cầnn thiết thì phải nhảy 2 dòng
Const RGDIT = "i3" ' ô bắt đầu dữ liệu cho đầu ra
Dim a As Variant, i As Long, j As Long, ia As Long, ja As Long
a = Range(RGNGU).CurrentRegion.Offset(RGNGUOFFSET, 0).Value
ia = UBound(a) - RGNGUOFFSET ' mảng dữ liệu thật ra nhỏ hơn vùng sử dụng 2 dòng
ja = UBound(a, 2)
For i = 1 To ia
For j = 1 To ja
If a(i, j) > 0 Then
a(i, j) = Log(a(i, j))
Else
a(i, j) = "#NUM!"
End If
Next j
Next i
Range(RGDIT).Resize(ia, ja).Value = a
End Sub
Có ai muốn thử viết code cho hàm Log hôn?
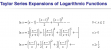

Mình cứ thế nghiệm giả định vào e^ làm căn cứ tìm nghiệm gần đúngTôi hỏi có ai hứng thử viết hàm triển khai Taylor của Log hay không bởi vì dạng bài này khá phổ biến với bài tập về lập trình.
Bài tập này được những người viết sách và dạy dùng để thử thách tư duy lô gic và vòng lặp của học sinh. Bình thường thì người ta dùng hàm Cosine bởi vì hàm này khá dễ khai triển. Hàm Log thử thách cao hơn một chút bởi vì nó có tới 3 dạng:
View attachment 259878
Hàm Cos chỉ có mọt dạng (vì vậy có thể dùng đệ quy thay cho vòng lặp cũng được)
View attachment 259879
(các hình trên cóp từ quép sai efunda chấm cơm)
Nó xoay thành bài toán: bạn dùng phương pháp trâu bò, đoán từ điểm thấp nhất trở đi hay dùng phép nhị phân, đoán 2 điểm?Mình cứ thế nghiệm giả định vào e^ làm căn cứ tìm nghiệm gần đúng
Bắt đầu 0 -> x ngẫu nhiên hoặc cho cố định ví dụ 10, thế vào e^ và so sánh kết quả: Nếu "gần đúng" thoát , Không bằng: Bước kế nếu lớn hơn là x/2 -> x ngược lại là x -> 2*x ...Nó xoay thành bài toán: bạn dùng phương pháp trâu bò, đoán từ điểm thấp nhất trở đi hay dùng phép nhị phân, đoán 2 điểm?
Vả lại, dùng phép tính mò như thế bạn phải đoán trước bước tăng đi của từng lượt vòng lặp.
Công thức Taylor chỉ xét lô gic, không cần phải đoán bước. Chỉ cần bạn tự đặt giới hạn "độ gần đúng"
Tôi không hiểu lắm. Bài #9 là thay vì tính log thì tính lũy thừa của e. Nếu thế thì tính luôn log thôi chứ tính lũy thừa của e thì cũng là con toán "khó như nhau". Tôi hiểu là ở đây tìm cách tính gần đúng log. Tức cách tính chỉ dùng các phép toán cộng trừ nhân chia. Phép tính lũy thừa bậc số tự nhiên có thể trình bầy bằng phép toán nhân.(*1) Cách tính nghiệm, và dùng thuật toán nhị phân như bài #9 là loại tính nằm trong bài học về thuật toán lập trình.
Function myLN(ByVal x As Double) As Double
Const saiso = 0.000000000000001
Dim k As Long, base As Double, base2 As Double, p As Double, result As Double
If x <= 0 Then Err.Raise xlErrValue
If x = 1 Then
myLN = 0
Exit Function
End If
base = (x - 1) / (x + 1)
p = 1 / base
base2 = base * base
For k = 1 To 10000 Step 2
p = p * base2
result = result + 2 * p / k
If 2 * p * base2 / (k + 2) < saiso Then Exit For
Next
myLN = result
End FunctionTôi thì thích cái Log(15#). Mong được chỉ rõ nguồn. Ngoài VBA thi cách viết đó còn dùng ở ngôn ngữ nào khác? Cảm ơnTuy nhiên, nếu gọi hàm này với hằng thì nên thêm # sau hằng để trình dịch khỏi phải ép kiểu Log(15#)
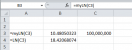
Các hàm triển khai Taylor là công thức gần đúng nên có sai số, nhiều khi khá lớn. Ví dụCode hoàn chỉnh.
Mã:Function myLN(ByVal x As Double) As Double Const saiso = 0.000000000000001 Dim k As Long, base As Double, base2 As Double, p As Double, result As Double If x <= 0 Then Err.Raise xlErrValue If x = 1 Then myLN = 0 Exit Function End If base = (x - 1) / (x + 1) p = 1 / base base2 = base * base For k = 1 To 10000 Step 2 p = p * base2 result = result + 2 * p / k If 2 * p * base2 / (k + 2) < saiso Then Exit For Next myLN = result End Function
Thực ra thì cách kinh điển của hầu hết các ngôn ngữ là gõ thêm một dấu chấm.Tôi thì thích cái Log(15#). Mong được chỉ rõ nguồn. Ngoài VBA thi cách viết đó còn dùng ở ngôn ngữ nào khác? Cảm ơn
Theo tôi, là For lặp ít quá. Tôi choCác hàm triển khai Taylor là công thức gần đúng nên có sai số, nhiều khi khá lớn. Ví dụ
Với vòng lặp lớn tốc độ rất chậm, vấn đề quan trong hơn là không khống chế được sai số ví dụ sai số cho phép là 10^-8 thì tới lúc nào thỏa và dừng code?Theo tôi, là For lặp ít quá. Tôi cho
For k = 1 To 999999999 Step 2
và in k sau khi vòng For thì k=740457257
và KQ khác nhau không quá 10^-7
Các hàm triển khai Taylor là công thức gần đúng nên có sai số, nhiều khi khá lớn. Ví dụ
View attachment 260450
Đó là lý do có tới 3 công thức, dùng công thức nào phải hiểu nguồn gốc của nó
Nguồn gốc thì dễ hiểu thôi. Cái lỗi là phải tính sai số theo công thức chứ không phải theo một số hạng nào đó của khai triển. Cái lỗi này không chỉ ở bài #14 mà còn ở bài #12.Theo tôi, là For lặp ít quá. Tôi cho
For k = 1 To 999999999 Step 2
và in k sau khi vòng For thì k=740457257
và KQ khác nhau không quá 10^-7
Khi dùng dãy số rời rạc tính một hàm nào đó thường kèm theo công thức xác định sai số, dãy rời rạc khác nhau sẽ có công thức tính sai số khác nhau và công thức nầy phải tính được, chưa hình dung nguồn gốc và cách tính Sai số R(n) = f(n)(c)*(x-x0)^n/n! như thế nàoNguồn gốc thì dễ hiểu thôi. Cái lỗi là phải tính sai số theo công thức chứ không phải theo một số hạng nào đó của khai triển. Cái lỗi này không chỉ ở bài #14 mà còn ở bài #12.
Công thức dùng trong bài đúng với mọi x > 0. Vấn đề nằm ở chỗ tính bao nhiêu số hạng thì dừng. Lỗi code là không tính sai số theo công thức mà lại dùng số hạng n làm sai số.
Thực ra sai số được tính theo công thức, và chỉ ngừng tính khi sai số nhỏ hơn cho phép. Không thể có số hạng nào đó nhỏ hơn sai số cho phép thì khẳng định rằng sai số được chứng minh bằng công thức cũng nhỏ hơn sai số cho phép.
Sai số R(n) = f(n)(c)*(x-x0)^n/n!
Trong đó f(n)(c) là giá trị đạo hàm bậc n tại điểm c, với c nằm trong khoảng [x0;x].
Nếu tính điểm dừng dựa vào công thức sai số thì điểm dừng sẽ nằm ở rất xa. Khi đó với k rất lớn như ở bài của bạn haog thì độ chính xác sẽ lớn.

Khi học về định lý, công thức, khai triển Taylor thầy và sách có đưa ra mà. Tất nhiên người ta phải chứng minh được thì mới đưa ra.Sai số R(n) = f(n)(c)*(x-x0)^n/n! như thế nào
Thực ra rỗi hơi thì làm tiêu khiển thôi. Nếu bạn muốn bạn có thể tự viết từ A đến Z rồi đưa lên cho những ai cần mà. Tôi không cần. Còn người khác có thể có người chưa chắc viết được code trên cơ sở vài từ chung chung của bạn. Muốn thì làm từ A đến Z rồi đưa lên thôi.Phương pháp nhị phân kiểm soát được sai số và số vòng lặp thấp hơn nhiều
Theo bạn nghĩ thì chính máy tính (và/hoặc các ứng dụng) làm cách nào để tính các hàm như Log, hàm lượng giác?Các hàm triển khai Taylor là công thức gần đúng nên có sai số, nhiều khi khá lớn. Ví dụ
View attachment 260450
Đó là lý do có tới 3 công thức, dùng công thức nào phải hiểu nguồn gốc của nó
