nguyễn thanh tùng3288
Thành viên mới

- Tham gia
- 2/6/21
- Bài viết
- 17
- Được thích
- 0
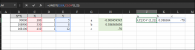
Xin chào các bạn! tôi có vướng mắc một vấn đề về cách tính phương trình bậc hai, tôi có 3 cặp tọa độ X,Y và cần tìm số của a, b, c.
Ví dụ: X1=300, Y1=5
X2=330, Y2=8
X3=410, Y3=12
tôi cần tìm X4 tại Y=10.
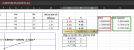
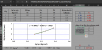
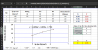
nếu vẽ đồ thị trên excel và hiển thị công thức đồ thị tôi vẫn có được các số liệu a, b, c cần tìm và nhập lại công thức tính sẽ tìm được X4, nhưng do file làm việc giải quyết rất nhiều bài toán trên nên nhập lại công thức sẽ rất mất thời gian, xin nhờ các bạn hướng dẫn tôi cách tính toán.
Xin chân thành cám ơn!
Ví dụ: X1=300, Y1=5
X2=330, Y2=8
X3=410, Y3=12
tôi cần tìm X4 tại Y=10.
nếu vẽ đồ thị trên excel và hiển thị công thức đồ thị tôi vẫn có được các số liệu a, b, c cần tìm và nhập lại công thức tính sẽ tìm được X4, nhưng do file làm việc giải quyết rất nhiều bài toán trên nên nhập lại công thức sẽ rất mất thời gian, xin nhờ các bạn hướng dẫn tôi cách tính toán.
Xin chân thành cám ơn!