Sử dụng Scroll bar và biểu đồ, giải bài toán tối ưu (1 người xem)

[hoangvietnhu]

Trong đời sống và kỹ thuật, nhất là trong tự nhiên,

sự phát triển của một cái gì đó, lại phụ thuộc rất nhiều vào sự phát triển của nhiều cái khác

Nếu lập mô hình toán học để dự báo, thì đại lượng ta khảo sát lại phụ thuộc vào nhiều biến số khác

Biến số, có cái ta biết được chính xác, có cái ta chỉ có thể giả định

Sử dụng thanh cuộn, để gán các giá trị cho biến số giả định là một biện pháp tốt

Sau đây ta giải một bài toán vui của học sinh cấp hai làm ví dụ

Bài toán này nhắc lại là

1/ Trong vườn có Gà và Chó đếm được tất cả là 36 con

2/ Lại đếm chân Gà và Chó có tất cả 100 cái chân

3/ Gà không con nào què và mỗi con đủ 2 chân

4/ Chó mỗi con cũng đủ 4 chân

Phần thưởng, sẽ thưởng cho toàn bộ số chân Gà sau khi nướng, nếu tính chính xác có bao nhiêu cái chân Gà

Lời giải

Bước 1: Lập mô hình toán học

* Với cách suy luận sơ khai, giả định Chó có 1 con

- Nếu Chó có 1 con, thì Gà có 36-1 con

- Ô A1 gõ SLCho, ô B1 gõ =1

* Nếu Gà có 36-1 con, mà Gà có 2 chân,

- Thì số chân Gà sẽ là (36-1)*2 chân

- Ô A2 gõ ChanGa.2, ô B2 gõ =(36-$B$1)*2 keó ngang công thức đến F2

* Nếu Chó có 1 con, mà Chó có 4 chân, thì số chân Chó là 1*4 chân,

- Mà tổng số chân là 100, thì số chân Gà sẽ là 100-1*4 chân

- Ô A3 gõ ChanGa.3, ô B3 gõ =100-$B$1*4 keó ngang công thức đến F3

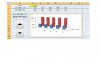
Bước 2: Vẽ biểu đồ

Quyét 2 dãy số liệu ChanGa.2 và ChanGa.3 ,vẽ được một biểu đồ cột,

một dãy cột cao 70, một dãy cột cao 96

Bước 3: Tạo một Scroll bar có thông số là

- Minimum value : 1

- Maximum value : 40

- Incremental change : 1 (Ở Excel 2007, hình như bước nhảy tối thiểu không được nhỏ hơn 1)

- Cell link : Đến $B$1

Bước 4: Lấy kết quả

Giờ chỉ việc kích vào mũi tên trên thanh cuộn Scroll bar để thay đổi giá trị ô $B$1

đến khi nào chiều cao hai dãy cột bằng nhau, là thoả mọi điều kiện của bài toán.

Nếu biểu đồ dạng đường, thì điều chỉnh khi nào hai đường trùng khớp vào nhau

Với bài toán tối ưu, biến số là giả định,

thì dùng phương pháp này nhanh chóng tìm được giá trị tốt nhất .

 

[hoangvietnhu]

Tram con Trau, tram bo co

Giỗ tổ Vua Hùng nghỉ dài ngày, thong thả lập mấy mô hình toán học. Trong khuôn khổ chỉ sử dụng chương trình Excel, mà không được theo cách giải lập hệ phương trình truyền thống

Ở đây mình ứng dụng thanh cuộn và biểu đồ để giải

Lấy bài toán vui : "Trăm con Trâu, trăm bó Cỏ, Trâu đứng ăn năm, Trâu lằm ăn ba, Trâu già một phần ba bó"

Làm ví dụ, xem tranh